Estimating RAS TSS
- Rick Fuller
- Sep 10, 2019
- 8 min read
Updated: Sep 27, 2021
Introduction
In this post I'm going to discuss how you can estimate the solids concentration in the return activated sludge (RAS) using the treatment plant influent flow rate, the RAS flow rate, and the mixed liquor suspended solids (MLSS) concentration. This approach is new for me, having read about it in a great, new textbook from Eric J. Wahlberg, described below. This post looks like it goes on forever, and it does, but only because there are so many graphics. Make yourself a nice, strong cup of coffee then take a look!

Favorite Textbook
My new favorite wastewater textbook is “Activated Sludge Wastewater Treatment” (Process Control & Optimization for the Operations Professional) by Eric J. Wahlberg. The book is published by DEStech Publications, Inc. (www.destechpub.com), ISBN No. 978-1-60595-333-5. This text is just loaded with insightful, useful information and I’m going to talk about a specific example in this post. The focus here is on information from Dr. Wahlberg’s Chapter 6: Secondary Clarifier. As part of this discussion I'll be using data from an industrial wastewater plant I visited recently.
As a side note, my job requires site visits to wastewater plants of all types. Either before, preferably, or certainly during my time onsite, I ask for as much laboratory/process control data I can get, hoping for at least the most recent year of data. How often I get the data I need and want, and how good that data is once I get it, is highly variable. But sometimes I feel like I’ve hit the jackpot, obtaining a wealth of detailed data, data that I can be confident in using to analyze and draw conclusions from. The industrial wastewater data used in this post is an example of a good data set!
Calculating the Return Activated Sludge Concentration
I want to start off by quoting from Dr. Wahlberg (Chapter 6):
“As observed by almost all operators who have conducted a settleability test in a settleometer or any container, very little continued settling (compaction) occurs after 30 min. While there are a small number of reported instances where the SSV60 is significantly less that the SSV30, for all intents and purposes the activated sludge solids are as compacted as they are going to be after 30 min of quiescence in a 2-L Mallory settleometer. From a practical standpoint, the maximum RAS TSS (TSSRASmax) concentration from the bottom of the secondary clarifier will not be appreciatively greater than the MLSS concentration in the settled sludge blanket after 30 min of settling (compaction) in a Mallory settleometer.”
Though I’ve been directly involved in wastewater treatment for more than 40 years now this view was both new and educational for me. I have always “assumed” that the sludge volume at 30 minutes was simply used as a short enough, but long enough, time period to allow the operator (me) to make an informed estimate (judgement, guess?) of how solids will settle in the secondary clarifier. I have always believed that a continued period of settling, 60 minutes or more, would result in a lower sludge volume, representing greater compaction. But how would I know this to be true if I always dump the settleometer and clean it after 30 minutes so I can go on to my next set of tests?!?
Dr. Wahlberg states that the return activated sludge (RAS) total suspended solids (TSSras) concentration can be approximated from the influent flow rate (Q), RAS flow rate (Qras), and the mixed liquor suspended solids (MLSS) concentration as shown in Equation 1.
Equation 1: Approximation of the RAS Total Suspended Solids
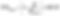
Dr. Wahlberg is making a very important point here, a point I have literally missed (not known or understood) my entire career. The RAS solids concentration is a function of flow, not the other way around, as is typically stated in other textbooks, and repeated by me, here, on this website. What I used to "teach," and have now removed from this site, are the two graphics below (Figures 1 & 2), each of which incorrectly shows how to calculate the RAS flow as a response variable to the solids concentration in the secondary clarifier, which Dr. Wahlberg calls "absurd." The book is worth buying just for the insight provided by Dr. Wahlberg's chapter on secondary clarification!
Figure 1: Aeration Tank Mass Balance to Calculate the RAS Flow Rate

Figure 2: Secondary Clarifier Mass Balance to Calculate the RAS Flow Rate

Putting Equation 1 To The Test!
Let's use the aforementioned data set I have to test how well Equation 1 from above, as taken from Dr. Wahlberg's book (Equation 6.6 in the textbook), holds up. I stated I had a "good" data set, not an "excellent" data set. From one year of data I had to do some data cleaning, deleting duplicate values, obvious data entry errors, etc. This is usually the case. Summary statistics for the return activated sludge (RAS) total suspended solids (TSS) concentration are shown in Table 1 from what I have left after scrubbing the data. That's why the counts are less than 365.
In Table 1, the two columns with the subheading "Actual" are the laboratory values measured by the wastewater plant. The two columns with the subheading "Predicted by Eq 1" are calculated from the actual values using Equation 1 from above.
Table 1: Statistical Summary of Plant RAS TSS Data (Actual vs Predicted)

Hypothesis Testing
From Table 1 it is easy to see that the mean actual RAS TSS values vs the mean Wahlberg-Predicted RAS TSS values are similar. But how similar? Are the differences statistically significant? I never rely on my judgement to make this kind of determination, particularly so because I have an excellent statistical analysis program called Minitab (www.minitab.com) that allows me to easily perform hypothesis testing. You can find a formal discussion of hypothesis testing here.
My null hypothesis is that there is no difference between the actual RAS TSS values and the RAS TSS values predicted by Wahlberg's Equation 1. The alternative hypothesis is that there is a difference and the difference is significant (two-tailed hypothesis test). In Figure 3 you can see the result of the hypothesis test produced by Minitab. In words, the conclusion is: The mean clarifier A RAS TSS for the actual data is not statistically different from the mean of the RAS TSS for the Wahlberg-Predicted data (p>0.05).
Figure 3: Minitab Statistical Test for Clarifier A RAS TSS

The same approach use for the clarifier A hypothesis test was used for clarifier B with a similar result. The mean clarifier B RAS TSS for the actual data is not statistically different from the mean of the RAS TSS for the Wahlberg-Predicted data (p>0.05).
The results of these two hypothesis tests are very impressive! For this particular data set Equation 1 works perfectly. The hypothesis test result from Minitab for clarifier B is shown in Figure 4.
Figure 4: Minitab Statistical Test for Clarifier B RAS TSS

The actual RAS TSS values compared to the Wahlberg-Predicted RAS TSS values for both clarifiers are shown in Figures 5 and 6.
Figure 5: Clarifier A Actual vs Predicted RAS TSS

Figure 6: Clarifier B Actual vs Predicted RAS TSS

The Careful Observer
The careful observer will note what seems to be very high TSS concentrations for the return activated sludge from the two clarifiers. Recall from Table 1 that the RAS from Clarifier A had a mean TSS concentration of 28,549 mg/L and Clarifier B had a mean TSS concentration of 22,433 mg/L. I found this plant to have some interesting operating characteristics that are worth taking a closer look at.
A simple process flow schematic of the wastewater treatment plant from which this data has been derived is shown in Figure 7. Note that this wastewater system operates as two identical trains in parallel. The major problem with the design of this system is the lack of true flow control to each train. Operators have to adjust the flow control valves based on trying to balance the MLSS concentrations in the two aeration tanks. There is no flow measurement into each tank. So any valve adjustment made today requires a day or more to obtain new MLSS concentrations to figure out if another adjustment is required. This makes process control very difficult.
Figure 7: Wastewater Treatment Plant Flow Schematic

MLSS Data
In Figure 8 you can see the concentration of MLSS for both aeration tanks. Not only are the concentrations on the high side, but you can also see how difficult it is to balance the MLSS concentrations between the two tanks without flow measurement available on the influent to each aeration tank. The operators aren't blind in trying to operate this wastewater plant but it is certainly hard for them to see what is going on in real-time.
Figure 8: Comparison of MLSS Between Aeration Tanks A and B

Keep in mind this is a conventional, plug flow, activated sludge system. According to Metcalf & Eddy, the typical MLSS concentration for this type of plant is 1,000 to 3,000 mg/L. Let's take a closer look at how the MLSS values are distributed across both aeration tanks.
In Figure 9 you can see the full range of MLSS values for aeration tank A. Note the 90% range which spans concentrations between 4,192 to 11,010 mg/L MLSS. (The distribution was fitted to the data using a software program from @Risk from Palisade.)
Figure 9: Distribution Fit to MLSS in Aeration Tank A

Let's adjust the limits in Figure 9 to span the expected MLSS range of 1,000 to 3,000 mg/L. The result is shown in Figure 10. How interesting! During the last year, at no time, was this conventional, plug flow, activated sludge plant maintaining an MLSS concentration in the appropriate range.
Figure 10: Aeration Tank A MLSS in the Proper Range

The picture is a little better for aeration tank B, but not by much. In Figure 11 you can see the full range of MLSS values for aeration tank B. Note the 90% range which spans concentrations between 2,363 to 7,560 mg/L MLSS.
Figure 11: Distribution Fit to MLSS in Aeration Tank B
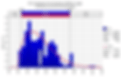
Again, let's adjust the limits in Figure 11 to span the expected MLSS range of 1,000 to 3,000 mg/L. The result is shown in Figure 12. During the last year this conventional, plug flow, activated sludge plant was maintaining an MLSS concentration in the appropriate range only 18.6% of the time.
Figure 12: Aeration Tank B MLSS in the Proper Range

Before ending this discussion on MLSS concentrations I'd like to make a few more comments. The well-known MLSS ranges from Metcalf & Eddy are specifically adapted from municipal wastewater treatment plants. Can they be applied to industrial plants? I would say yes because I'm not aware of a set of process control parameters specific to industrial plants so we don't have anything else to go by. A major reason for this is that the wastes generated by industrial systems are so different as you move from chemical to pharmaceutical to refining to steel and so on. I just do not recall ever seeing an industrial system using conventional plug flow activated sludge that operated with an MLSS range between 1,000 to 3,000 mg/L. Many of these plants operate in a range of 2,500 to 5,000 mg/L MLSS and they operate very well.
Therefore, I wanted to provide two more iterations of the MLSS distribution fits using the more common range of 2,500 to 5,000 mg/L as shown in Figures 13 and 14. With this broader, more realistic range you can see that the MLSS concentration in tank A is still excessive, fitting into this broader range only 21% of the time.
Figure 13: Aeration Tank B MLSS in a More Common Range

Using the broader range of 2,500 to 5,000 mg/L, the MLSS concentration in aeration tank B is now appropriate 62% of the time, a dramatic improvement from the lower range referenced using Metcalf & Eddy. The wasting rate is not as high as it needs to be for optimal process control, but the MLSS concentration in this tank indicates far better process control than what is exhibited by the MLSS concentration in aeration tank A.
Figure 14: Aeration Tank B MLSS in a More Common Range

Final Observations
The high total suspended solids concentration in the return activated sludge from both clarifiers can partially be explained by the presence of excessive inert material in both MLSS streams flowing to the clarifiers. In Figure 15 you can see that the mean MLVSS/MLSS ratio is 59% for both tanks. This is low. Further down, in Figure 16, you can see the expected range for the MLVSS/MLSS ratio, which spans 60 to 85 percent. (I use 72% as an estimate when I lack data.)
Figure 15: Aeration Tanks A and B MLVSS/MLSS Ratio Data

Figure 16: Expected Range for MLVSS/MLSS
